A New Direction

In this project I look at the various ways a fourth dimension can exist or not exist. Specifically: the topics of time and space as a dimensions are deeply discussed, along with the applications and purposes of looking at dimensions in this way.
Grade 9

Problem

Question: What are the principles of movement in the fourth dimension?

Why To Care: 

Several reasons can be provided about why this grand topic requires study and inquiry to make the future of humanity better, and to make science more complete in understanding. As discussed before - a large theory of the universe lies in the hands of new dimensions being discovered, and this will lead to the more complete theory of string theory, but can also provide a new approach about how the universe works. Further developing theoretical evidence, and even experimental evidence, will provide the future of physical theory for the nature of the universe; replacing string theory, or establishing more ground on it. Not only will science benefit, but also mathematics will significantly benefit from the concept of new dimensions, especially in the aspects of things like cross-sections, vectors, graphs, shapes, and many other necessary parts of applying natural phenomena with mathematical equations. Plotting graphical systems with more than three variables can result in the understanding of more complex systems using mathematics, which applies the graphical sense of four dimensions and higher. But: for so long now have physicists trying to be sure of what the idea of a fourth dimension means and can be. Which means when everything comes together in one big consensus of incorporation and information, scientists can prevail in joy and happiness, and this will become a big accomplishment of humankind and the capabilities one species has. But: even going past that, these kinds of abstract definitions and endings can actually appear in unknown places that almost would make no sense, like how the imaginary number "i" appears in the Schrodinger equation. That number is an abstract definition - even called imaginary - and was only really made to solve some solutions in mathematics, but eventually appeared in very important physical science theory; and using these conclusions: a fourth dimension may also apply in a similar way towards the future of sciences in other fields. Unfortunately, this can be hard to apply to everyday life. Although: the discovery of fourth dimensional thinking could influence technology in a way that would most definitely benefit even the everyday person who understands nothing about the important theory and process of using these applications of the fourth dimension. Once everything is understood, the idea of why it even needs to be studied absolutely comes into mind: but this specific topic has many justifications to rigorous experimentation and theoretical business.

Hypothesis:

I predict that when principles of movement are applied to the fourth dimension, the mathematics and ways that describe how it works will significantly change. This will not be specific to the coordinate system of it precisely, but directly towards how it will be described using the human mind. New tactics will have to be applied to help the movement become more clear towards the human brain, which is implied to be impossible to imagine what 4 dimensions appear to be. A main reason for why this is true is because of this impossibility to visualize the fourth dimension, and especially movement within the fourth dimension.

Method

The methods of research used were conducted in these three methods, ordered from most used at the top to least used at the bottom:

  1. Research from the internet, in forms like learning websites such as "Khan Academy", and published documents and websites like "Popularmechanics"
  2. A more knowledgeable person by the name of "Sebastien Wagner" in his second year majoring in astrophysics at UoC
  3. Videos from youtube from sources like "TedEd"
  4. A book called "Our Mathematical Universe" by Max Tegmark

Overall, these methods of research combined together to make a cohesive and understandable project about the fourth dimension. Keep in mind that some of these paragraphs are more directly from sources, and others are made by using other information and making proper judgement for what to write.

Research

       Definition of a Dimension

 

To start off, much of the information can be stated from initially understanding what a dimension truly means. In the simplest terms: a dimension is a direction of movement, perpendicular to other directions of movement. Moving around in a space conducts through these dimensions, and they describe position in the universe. Unfortunately, all of this position using units and numbers requires a position to be relative to. Everything has to be relative to a position in this area as a center origin, and many areas can be this center; in astrophysics it could be the center of the Milky Way, or in geography it could be the combination of the prime meridian and equator. For the most part, life of humanity is conducted within three dimensions: three perpendicular directions; and these are described using the x, y, and z axes. But keep in mind that polar coordinates - ones that use a distance from the origin, and as many other angles from a dimension are needed - also exist. Take into account a model, having an imaginary origin as a giant sphere (in reality it is a zero dimensional point). Using the giant sphere to attach a pole to the end would show the addition of a first dimension, and adding one perpendicular to the first pole will allow a second dimension to exist. Keep in mind that these poles represent an infinitely small radius, which means by itself, they are first-dimensional. Lastly, it is possible to add one more pole that will be perpendicular to both of the previous poles: this makes the third dimension. A perfect representation of what is lived in can be shown here, and when labeled, a coordinate system can be created. Simply, and elegantly: this definition of a dimension helps take into account how the world is created, and what different levels of dimensionality mean.

Image of polar coordinates (left) and cartesian plane (right).

 

Definition and Properties of Previous Dimensions

 

It is well known that existence is played out in three dimensions, but pondering what previous dimensions would look like can help with the understanding of higher dimensions. 

 

  • Zero-dimensional space takes place in a single point that is infinitely small in width, height, and depth. Movement in these restrictions is impossible, and if a higher dimensional object passes through (objects are practically impossible in zero-dimensional space): a sight of change will be unidentifiable, and no information can be transferred. 

 

  • One-dimensional space is a little more exciting, with exclusively an x-dimension. Length here is infinite, and life would be conducted by moving positively or negatively in the x-dimension. Geometry here is strictly made of up lines; which can be of things like the length or distance away from another point. With sight existing in this dimension, everything would be zero-dimensional in perception, and length or distance away can be shown with brightness or other properties of colour/light. A two-dimensional object or higher-dimensional object passing through would appear to change in distance away from a point quickly; this would be from nothing, to something, to nothing.

 

A one-dimensional line segment.

 

  • Two-dimensional space is the final lower dimension, and it uses axes of x and y to determine the length and width of objects. Geometry here is concentrated within Euclidean definitions, and every object has a depth of 0. Everything from trigonometry to drawings are concentrated here with certain widths and lengths, which also spread to vectors that must contain two to describe all objects (like Fx and Fy). Flatland is a novel by Edwin Abbot Abbot which describes what it would be like to be in two-dimensional space, and it uses one-dimensional vision with perception of distance away. Sight in this world is conducted through concentration of hue and distance long, but infinitely thin sight. Imagine a three-dimensional sphere. From traveling through the plane: the three dimensional object like a sphere would appear to start very small as a circle, then expand in length with a brightening hue, and then reverse the actions back away. Common geometry also takes place here with a square having four edges, and one face; this is unlike before where there is only one edge possible. 

 

It is evident that the expansion of knowledge greatly increases through making the dimensional space greater, and looking at the smaller will give knowledge and predictions towards the larger.
 

What it Means to Be In Three Dimensions

 

Being able to understand the three dimensional space lived in gives an understanding of the current world around, and this provides explanations for many of the natural phenomena of the universe. Geometry in this three dimensional space consists of x/length, y/height, and z/depth axes; which determine every position within the possible universe as of current understanding. Vectors must take into account the individual positions of three movements, using more advanced trigonometry than needed for two dimensions. These vectors would be Fx, Fy, and Fz. Squares are expanded into cubes at this point, which contain 1 three-dimensional face (more on this later), 6 two-dimensional faces, 12 edges, and 8 vertices with infinite points along the edges and so. Humans see within two dimensions, and use two eyes to perceive depth and distance within the two dimensions visualized. Seeing in this dimension also means that lower dimensions seem much simpler and non-working, but it also makes further understanding and visualization for higher dimensions practically impossible without any kind of simplification. It could seem that it is impossible for higher dimensions to also exist. Understanding these meanings of the few dimensions before the third  can imply understanding towards formulas and other principles of higher dimensions and the dimension humans live in.

 

Principles and Mathematics of Three-Dimensional Movement

 

Understanding some of the principles of movement of the third dimension can help with the discussion of higher-dimensional movement. All of these equations will assume euclidean three-dimensional movement, along with them focusing on movement at speeds not near light-speed - some relativity explanations will also be provided in later sections.

 

Note for the online section: Equations in here have been significantly degraded due to the writing platform on the website, they are more appropriately formatted within the tri-fold

 

  • F=ma (A)

 

This equation is one of the most basic equations in physics, and has to be divided into separate vectors to express dimensional movement above one-dimensional space. Force is described with the F term, mass is described using the m term, and a is describing the acceleration of the object. Representation of units uses kilograms as mass (for these cases), uses m/s2 for acceleration, and newtons ((kgm)/s2) for force. 

 

  • p=vm  (B)

 

Momentum is described in this equation as the p term, but this specific equation describes the change in momentum. The “” term represents change in, as the greek letter delta. Change in velocity is also represented by the v, and mass is described without a change in (it assumes that no mass is changed). Velocity is represented using the units of m/s and momentum uses the units of (kgm)/s. A change in momentum would represent an increase or decrease in overall momentum of an object, and the sense of momentum is how hard it is to stop or start moving an object.

 

  • KE = (1/2) mv^2 (C)

 

Representation of kinetic energy is provided above, in which KE is kinetic energy, m is mass, and v is velocity. Units for kinetic energy are joules (J) which can also be described as newton meters (Nm) - where the m in newtons becomes squared. Kinetic energy is one part in describing mechanical energy, which is the equation describing the energy in the motion of objects. Using this equation will aid in understanding other quantities of objects: like momentum, acceleration, force, and more.

 

  • PE= mgh  (D)

 

Potential Energy is the quantity of energy that can be produced when released from the position it is held in. In this equation, the acceleration is the g term - which stands for the gravitational acceleration on Earth. Quanities of this kind of potential energy can only describe some potential energy applications. The only other new term here would be the h, which describes the height of an object where the potential energy is directly away from, like distance from the center of a planet for gravity. Meters are the proper unit for height though. 

 

  • ME=PE+KE  (E)

 

The sum of potential and kinetic energy make up the total mechanical energy, which is one of the main energies used in physics; along with other important ones like thermal and electric. Using this equation can easily help determine another term of energy, and many variations exist. Most of these variations are due to the addition of external work to the system the process is taking place - the system is the objects and forces considered when calculating and observing an answer - which can be added in many places. An example would be if air resistance caused external work on a skydiver, who transferred all of their potential energy into kinetic energy when reaching the Earth’s surface. An equation would then be KE-W=PE, where W is external work done by air resistance.

 

  • d=x+vt+(1/2)at^2  (F)

 

A great representation is provided towards the distance an object travels in an interval of time, and it can be manipulated to describe many more things. Distance here is represented by d in meters, x is the initial position based on the origin used, delta t is supposed to be the change in time, and v is supposed to be the initial velocity. Units for x and delta t are respectively: meters and seconds (longer time intervals are possible, but units change). So, if acceleration is constant, this equation can describe proper distance. Most of the time, it is used to determine something from rest - where the initial velocity and position is zero. Like as if you wanted to determine the gravitational acceleration of a planet, you could use a stopwatch and large ruler to determine the acceleration, this would use a variation of this equation as 2dt2=a. 

 

Example Problem using Equations to Clarify:

 

Take this into account: imagine an object that has a constant acceleration of 2 m/(s)(s), this object would also have a mass of 5kg. After traveling for 5 seconds, the object changed from rest to a velocity of v. What is the distance traveled, velocity, kinetic energy, force, and momentum of the object?

 

Solutions:

 

F=ma , F=(5kg)(2m/(s)(s)) , F = 10N

 

d =(1/2)at^2 , d =(0.5)(2m/(s)(s))(25(s)(s)) , d=25m

 

v=at , v =(5s)(2m/(s)(s)) , v = 10m/s ,

 

KE = (1/2)mv^2 , v=10m/s , KE=(0.5) (5kg)(100(m)(m)/(s)(s)) , KE=250J

 

p=vm , p=(+10m/s)(5kg) , p=+50(kg)(m)/s

 

Overall, the equations used were simplified in process, with neglecting negative numbers in the vectors, and more advanced applications can be made with conservation of energy, elasticity, and other impacting quantities and qualities. Like when multiple dimensions are used, trigonometric equations like cosine and sine may have to be used to determine the quantity of a vector in a certain dimension: this is the only possible way to achieve motion properly. In general understanding these basic principles will aid in the understanding of further dimensional equations and movement. 

 

Two Editions of What a Fourth Dimension is

 

During the research process of this project, it was discovered that there are mainly two types of the fourth dimension that are widely accepted. The first of these is the idea of time as a fourth dimension, which was suggested by Einstein to understand the dimensions of spacetime. Much of the understanding in this idea commences from the concept of special and general relativity, and they also allow for many predictions to be made about movement spatially, and time’s speed. But, this theory is more widely accepted, it has been explored for longer; therefore offering more of its theory to explore. Another way to see a fourth dimension is through the use of higher spatial dimensions, where the possibility of even higher than four dimensional objects exist. Possibilities expand here with the creation of branes, string theory, tesseract, and many more confusing yet enticing concepts. Unfortunately, the idea of this is much more controversial, with people trying to see if it is even real: resulting in a scatter of belief, disbelief, and several theories. Objectively, it is also understood that there are many viewpoints for a person to have about these theories, which will be explained later too. In general, the two main possible theories for a fourth dimension were prompted to be explored through the use of many resources claiming the existence of it.

 

Relativity and One Fourth Dimension

 

Relativity in general explores the idea of position and being at rest, which build the fundamental theorem for how space and time works. Take the idea of Earth’s gravity for example, along with a box accelerating in empty space at the acceleration of Earth’s gravity. Without any extra information like air resistance, terminal velocity, sound, or light: it would be impossible to know exactly which box you are in, the one falling down to Earth, or the one accelerating upwards. Explanations will involve relativity, with two main rules being explained: you are at rest in your relative frame - no matter what situation one may be in - and light’s speed is always constant no matter what circumstances. Now, also established in this theory is that there is a fourth dimension: time. In this context time is perpetually moving forward, as far as current science and technology goes, there is no way to reverse time; but there are ways to change the speed of progression of time. Spacetime is the combination of both space and time, which allows for an understanding of how humans and other objects move and change through the progression of time and movement. One diagram is provided, which is a representation of a space-time diagram - where the x axis is space in one dimension, and the y axis is time - the red line represents an individual who would remain stationary in frame relative to anyone else who is non-moving. Unlike the red line, the blue one represents an individual who travels through space and time, and they would move much more than the other individual who sees them travel light-years away, and then return in 8 years. Calculating the numbers here interprets that the amount of spacetime-units (stu=yly, but the units here are different than normal, with ly as light years and y as years) traveled in the period of time as 8 light-units for the red line, but 10 light-units (using 3-4-5 triangles) for the blue line. Some simplifications are made to avoid more complex solving, like how time at the speed of 0.75c will move even slower than the normal time an individual travels up on Earth. Which also can be interpreted as saying that the higher one is in a building, the slower time moves around them; this is the concept of time dilation. Although these complications exist, it still shows the grand understanding of moving through the four dimensions of understood spacetime. Summing it all up, understanding the theory of relativity can assist in understanding a more mainstream theory of a fourth dimension, which will in return give insight into the beginnings of how space and time interact. 

 

Why Time is A Dimension

 

Understandably, one may be confused with the grasp of information presented; but an explanation of how time even becomes the fourth dimension can help clear the fog. It can be already known that time is always moving forward, and can be completely described visually using just one one-dimensional line with events in history, current, and future affairs being plotted on it. But: time is always moving forward, and can only be slowed down by traveling at near light-speed velocities, with a magnitude and direction. A small section of argument was just made there as to why and how it can be a fourth dimension, as it can be altered and described in many ways that share similarities with the idea of a dimension. To help clarify: imagine an object being moved through a three dimensional space, in this space the cube moves through the space as it moves through time. Without time, it would be impossible to move the object, give it an acceleration, or have a capacity to hold and output momentum. More or less, to describe this new dimension, it requires a graph in three dimensional space, along with a one-dimensional line to plot when and how long a movement in that space may last. Pushing the boundaries of what a dimension is can also be included in the understanding of time as a dimension, which is because it does not have a reverse or negative direction to move in. Even though this asterisk exists, it does not deny the fact that time is a dimension, especially because no one is one hundred percent sure that time travel is impossible, but do not take this idea too far; because it could also easily be impossible. Journeying into that kind of theory is unnecessary, but there are better well-established reasons why this is possible too. Like how the theory of many bizarre things like wormholes, white holes, and other crazy astronomical phenomena describe this possibility. Generally it is hard to grasp the idea that time - yet spacetime - is a four-dimensional space where everything takes place in, but the explanation provided helped make it more clear and visible that this is true.

 

Connection to Time and Space

 

A connection can be made between space and time, which allows for the future of movement and mathematics for physical to barely tangible objects to work in the all-encompassing spacetime as a four-dimensional space. Spacetime itself operates sort of like a large trampoline with grid lines to describe areas with the same space and time together. Imagine a marble being placed on there - this would represent a smaller celestial object like a planet - which warps the trampoline surface around it, and makes it so other smaller objects are more easily attracted to it when rolling nearby. Now place a bigger object like a large medicine ball, the warping around this object with more mass is more significant, and objects fall into its influence much easier. This is what spacetime is, the physical medium that is altered and shifted to make time move much slower for those under greater influence, and attraction is achieved through gravity at a cosmic scale, instead of a human’s scale. More massive objects make greater indents in the fabric of spacetime: it also makes a greater acceleration, a greater escape velocity, and the effects of collapsing in on itself when it becomes too great into a black hole. Everything known reflects several properties in this medium, which is also around everything, but on Earth the gravitational pull of itself is too great to actually allow for human’s gravitational pull to be significant enough for other things to get attracted greatly. Cosmology also has a great benefit from this idea through the formation of the early universe, which made the gravitational force a thing, and allowed for the space to become much less compact and dense. Time dilation is another big impact of this deformation in space too. When speeds near-light speed are achieved or when orbiting a massive object, time dilation will impact the proceeding of time; specifically in these situations the faster or more massive the object: the slower time will move on. Providing another detail about how this impact also relates to the idea of going faster than light, and the impact of the passing of time when that is achieved, but as far as scientists currently understand: this is impossible. Majorly: the connection between space and time to form spacetime creates much of modern-day theory, and creates understanding of the various intricacies of the universe from macroscopic to microscopic.

 

3D representation of spacetime curvature.

 

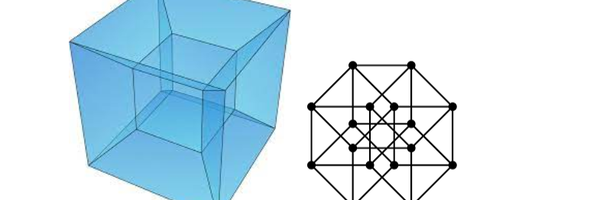
Another Direction to Move In

 

Now onto a little bit more of a debatable statement, the idea of a spacious fourth dimension is an idea focused on the concept that there is something that humans as a species are unaware of. To introduce this new idea, most people have added an extra letter to the coordinate system, along with another perpendicular; such as when it is defined as the “w” axis, or as the strength (as of width and height). Creating this fourth dimension will have to occur from using existing patterns from previous dimensions, which somewhat follows around a 2p pattern, with p describing a p-dimensional object. Explaining this deeper: a zero-dimensional object has one point, a one-dimensional line segment has two points, a two-dimensional square has four one-dimensional lines, and a three-dimensional cube has six two-dimensional squares. Adding onto this previous understanding gives the insight that a four-dimensional object will have eight cube faces, and what is described here is a hypercube or a tesseract of a cube. Using other patterns will also describe more features of a hypercube, like it having sixteen corners, twenty-four two-dimensional faces, and much more. Other shapes can also be expanded into four-dimensional space, like making a hypersphere, a hyperdodecahedron, or a hyperpyramid. Names for this type of object vary a lot, like the examples used can be polytopes, hypersolids, tesseracts, or higher-dimensional counterparts. Extending into this new dimension offers many opportunities for the concept of cross-sections to be understood in other ways, because it mainly focuses on what polygon will be produced when a plane moves through an object. If it is recalled from earlier, using these cross-sections is how understanding what the third dimension looks like moving through a second dimension. Problem solving with this idea will lead to the idea that a four-dimensional object like a hypersphere through the three-dimensional plane will look like a sphere growing in size from nothing - reaching a maximum size - then shrinking back to nothingness. Cross-sections can also be described in other ways which establish the idea that cross-sections of a four-dimensional object are a three-dimensional object. Take the hypercube where the three-dimensional cross sections can be tetrahedrons, rectangular prisms, octahedrons, and right isosceles triangular prisms. Understanding the true grasp of a fourth dimension spatially can help adjust to the possibility of an ever higher dimensional space that humans have no conceptual understanding of.

 

 Two representations of a hypercube.

 

Image describing the addition of dimensions to others, but this also applies to time as a dimension.
 

As a footnote, keep in mind that higher dimensional objects also can assist with other topics that will be explained later. To assist take in this diagram of what a dekeract or ten-dimensional cube would look like. But, keep in mind that it is very simplified as being in two-dimensional space, and describing an object eight dimensions higher.

 

Heavily simplified version of a dekeract. 

 

Searching for the New Direction

 

String theory gives an observation to how a higher dimensional plane might even exist in the first place, but is riddled with many intricacies and problems to solve; which can be interpreted as theories needing to be added on. Gravity as a concept was not really established as a central force of the universe in quantum mechanics previous to string theory, and it was impossible to add it without causing significant problems. Other forces that were already integrated would be like the electromagnetic force, the strong nuclear force, and the weak nuclear force. Introducing string theory solved the problem with a whole new concept, and established gravity as a central force in the universe’s functions, but this posed a problem: now there would have to be ten dimensions at least to make it all work, and there are no exceptions. Therefore, proving the fourth dimension could offer a helpful hand in establishing string theory as a better holder of current understanding in physics. Branes are the central concept that allow string theory to actually connect the universe in an unconventional way, and these branes are the plane that the human world of three-dimensional space takes place on. Expanding past the brane are the strings that connect space together - which were established in the very early universe - and they go beyond the plane of existence. Four-dimensional space or higher is what is contained outside the brane, and p-branes describe the amount of dimensions that are on the brane, like a three-brane for three-dimensional space. Now to connect parts of the third dimension together in odd ways, strings are established and lifted out of the three-dimensional space, and connect to another place in the brane; these are made out of fundamental matter - not exactly stuff scientists know about - but they are most likely quarks in current understanding. Also included in the theory: particles that are the most fundamental are made out of these strings following vibrations that determine properties. Unfortunately, most of the dimensions visualized in the concepts of modern quantum mechanics predict that the new dimensions will be very small in size - but luckily not all (the biggest at around a cube centimeter, and smallest at the atomic level). Combined together, all of these observations form the theory of string theory, which establishes the principle of a fundamental change in the idea of understanding the possibility of higher dimensions.

 Simple string theory diagram describing banes and strings.

An Objectively Correct Version?

 

Both of these explorations into the idea of the two currently most accepted theories of higher dimensions present arguments for the existence of them, and the arguments against their existence or legitimacy. Most of the arguments were varying in the sources used, and opinions will also be expressed from the expert being contacted. Each argument here will include the shortest summary possible without cutting out any of the very important details, and it is absolutely important to try and agree with a position and state the most convincing part of it.

 

  • Existing: time dimension

 

Einstein's theory of relativity established time as a dimension, which is highly accepted, and probably the most out of all of these ideas here. It was very easily enforced when the best theory to describe so many of the universe’s fundamental functions are correctly understood in the theory. Usefulness of thinking of time as a dimension has also proven worthy in many problems involving relativity, light cones, and other important principles in the understanding of the many intricacies of spacetime.

 

  • Existing: spatial dimension

 

Most people trying to prove this believe that string theory is correct, and that if this idea of a higher dimension is possible, string theory can become the dominant theory. Their argument focuses on that if string theory was the best application of gravity to become a fundamental force: then it must be real. And another point established is that the universe would not just stop at three dimensions, if patterns can go on then it could possibly go forever.

 

  • Non-existing: time dimension

 

Shortly, this idea of a non-existing time dimension is much more removed upon scientific observation: so the idea of it not existing is much less believed. Mainly, this idea just focuses on the fact that time is so fundamental that there is no need for a dimension to actually exist to describe it, unlike Einstein proposed. Very quickly, this falls apart when more than one time dimension is added though.

 

  • Non-existing: spatial dimension

 

The argument surrounding this part mainly focuses on the fact that there is no definite fourth dimension - like how it is impossible to be sure which cup of water was first in a jug full of 2 or more cups of water. So this entails that there is no definite fourth dimension, but instead just four or more dimensions. A more definite answer to it not existing would be contained in the fact that people think that there should not be ten dimensions (nine spatial and one time) in string theory, and try to make new theories out of that principle.

 

Overall: the understanding of various agreements and disagreements of the theories provided can help form an opinion about the specifics provided, and these are the most accepted ideas of a fourth dimension.

 

Math of Static Position in Both Further Dimensions 

 

Static position is defined as being still and non-moving in the third dimension, and expanding this concept to the different ways a fourth dimension exists may promote certain aspects of the current world. Mostly, everything about the time dimension does not overall change that much when being added to the previously known third-dimensional space, but it does add to the fact that it is sensible to describe it as a dimension. When time is unmoving: an object is unchanging, and this also somewhat applies in reverse. That means that the best way to describe a static object using time as a fourth dimension is to describe coordinates of the spatial parts using x, y, and z; then describe time using a variable t. Because of the long essence of time, the part that could be considered the origin of time would be the start of time at which a certain object came out of rest. Other time measurements could also be using longer or shorter periods of time which could contain: years, centuries, microseconds, and many more ways to accurately represent the static position of an object relative to time and space. Describing the position in spacetime graphically could be achieved using a limited range of the spatial axes, and time can be described off to the side in which another range of possible units and values are possible. Keep in mind that whenever time is described, it can only move forward when an object is moving through the space provided. When communicating about a spatial four-dimensional space: another axis is added, this is the w axis (preferably, one might want to use ), which can describe a position that is unable to be seen through human eyes. Unchanging objects not unclear in a way due to the w axis can be described using the value of zero on this axis, which means that possibly everything visible and understandable to the human species has a value of zero on this axis. Luckily, some objects can also move in the fourth dimension, and not be altered by the lack of human ability to see it - for example moving a hypercube through human space will stay the same in a human’s perspective for as long as its certain dimensions can handle it. Further extending this: a three dimensional cube moving through a two dimensional plane will suddenly appear as a square, stay there until the side length has been fully moved through, then suddenly disappear (this is also similar to a rectangular prism). Generally: only the idea of the x, y, z, and w axes are really needed to give the idea of four spatial dimensions existence, but understanding the realm of how it applies to sight in three dimensions adds depth. And overall, understanding the realm of static position in two definitions of four-dimensional space give insight to how it could currently apply to further understanding.

 

Dynamic Movement Mathematics in Both Dimensions

 

Now, an exploration of how equations may change in both definitions of another dimension will be applied. Each equation from before will be listed as a letter, along with a change for each of the dimensional applications. And the letter S will specify a spatial application, and T, a spacetime application. Some of these equations can be unchanged.

 

  •  F=ma  (A-T)

 

This equation does not change significantly when applied to time, but now that time is a dimension, acceleration is now a product of more vectors. Einstein's principles lead to the change of this equation to better fit near-lightspeed velocities, which was aided by thinking of time as a dimension. Specifically, this assistance was made with the slowing down of time at these velocities.

 

  •  F=ma  (A-S)

 

Not much changes are made, but now there is another vector to apply to when using an uneven direction. Which means observation tricks must be made to help understand how the dimensional vectors using sine and cosine must be applied, along with the understanding of how it may appear in three-dimensional space.

 

  • p=vm  (B-T)

 

Velocity now becomes more of a vector type quantity, along with Einstein's equations playing another major role in understanding: but momentum is regarded as less important than other quantities and directions.

 

  • p=vm  (B-S)

 

Along with the last spatial change, this one would also require more advanced understanding within the premises of how one thing may move, but this quantity can be changed to focus more on how long an object may stay within human vision - such as: vwV=t. In this equation it describes the amount of time an object would spend in human vision depending on the velocity in the w direction as v subscript w, the side volume of the rectangular prism tesseract as V, and the time spent in human vision t.

 

  • KE = (1/2)mv^2  (C-T)

 

Kinetic energy in this kind of situation now has to apply to the same rules as previous time dimension equations discuss.

 

  • KE = (1/2)mv2^2 (C-S)

 

In this equation, vectors need not to apply, so the idea of a spatial fourth dimension does not add much, and only add a possibility of one confusing trigonometry situation. Vectors more specifically do not need to apply here because kinetic energy itself is not a vector.

 

  • PE= mgh  (D-T)

 

Not much changes with the addition of time as a dimension within this equation, and this is due to the fact that acceleration is the only part of the equation that uses time in its units. Because potential energy can change rapidly, it is better to use it in a graph comparing kinetic energy, potential energy, and time. 

 

  • PE= mgh  (D-S)

 

Like the addition of time as a dimension, another spatial dimension does not change this equation much either. Especially: this applies also to due the non-vector quantity, and how it rapidly changes.

 

  • ME=PE+KE  (E-T)

 

Due to the idea that the addition of scalar quantities makes another scalar quantity, this also is not changed significantly, and can really only still be used to describe a total of two quantities in non-dissipative situations.

 

  • ME=PE+KE  (E-S)

 

Adding a fourth dimension into this equation likewise does absolutely nothing. Unfortunately, along with its non-vector properties, it also does not describe anything that can be altered with this addition. 

 

  • d=x+vt+(1/2)at^2 (F-T)

 

Time as a dimension makes this equation very different. Generally, this equation uses time very significantly to describe the exact position of an object traveled, so making that change will result in many graphs to consider time as part of the movement more so. Vectors also apply to this equation in every variable, and make another contribution to the idea of time as relative and changing in speed when traveling at certain velocities.

 

  • d=x+vt+(1/2)at^2  (F-S)

 

Spatial dimensions in equations where the vector is very significant - like this one - will allow for certain uses of trigonometry to apply to the direction exactly moved in. Proposing a change in the direction of acceleration with an alter in the numbers and composition of the equation can also allow for acceleration to change in direction in new dimensions. Easily, this can be described using the addition of a graph to give change in acceleration.

 

In general, changing these equations to include the concept of a higher dimension in both ways to alter space and time result in some insignificant changes, along with significant changes in how it may work.

 

How This Contributes to the Shape of the Universe

 

After taking understanding into the idea of a spatial fourth dimension, the idea of how the universe humans and other organisms live in can present some treachery, but with more understanding: a future of what the universe is shaped like can be determined. Euclidean geometry describes geometry assuming that all of it is done within a flat two-dimensional plane, where there are only one type of parallel lines. Taking that and extending it into further space: if the plane is altered into a sphere, all of the angles in a triangle would add up to 270 degrees due to the alteration, along a hyperboloid: a triangle could add up to only 100 degrees in its interior angles. Respectively, these form a convex and concave universe for two dimensional objects, assuming the plane folds around to form it. For the hope of a euclidean geometry census, a cylindrical object can also represent a triangle with the general rules of angle addition, but still: there is always this specification that could be added to most problems involving triangle angles. Now take this idea into consideration for the fourth dimension spatially, if the plane that humankind lives on is curved in such a way that any of these occurrences happen, it could mean much for modern and future geometry, along with cosmology. More so: it would be pretty hard to imagine a place where the universe stops and nothing exists, so if there is a certain boundary where the universe comes back on in itself, it would make much more sense, and all of these objects would allow for this: even in the fourth dimension. But these ideas also move past just a place where one can return to the same position by initially moving away. Space is known to expand, but using these ideas and concepts the four-dimensional objects are accelerating in size, resulting in the expansion of space that is minimally well-known. And understanding the ideas of how the expansion’s idea changes to relative frames also adds too - these two are: galaxies are moving, and space itself is expanding. If this object humans live on also is an expanding object that connects in areas in the fourth dimension, then there is a third reference in the space moving out of the plane and into the four-dimensional space outside of w = 0. Lastly, the other effect of this change is that the shape of the universe can be various things. Four-dimensional hyperbolic paraboloids are even on the table for the specific shape of the universe where there is a region with more angle measure possibility, and another area where the angle measure gets shorter. Other shapes like a four-dimensional torus where in any direction moved, one can return to their initial position just by going in a straight line, and allows for general geometry to exist. Unfortunately, this could also be interpreted as some spaces ending up with three dimensional geometry where angles and sides also do not match; like how there are multiple parallel lines in a hyperbolical space, there could be multiple non-connecting infinite faces in the space humans exist in. Summarizing the content provided: the extension of a fourth spatial dimension results in the concepts forming that can predict the extension of geometry when current humans know it.

 

 Hyperboloid (left), cylinder (centre), and shpere (right); all of which are described in the concept of eucalidian geometry existing or not.

 

 A parabolic hyperboloid - or as most people know it: the shape of a pringle.

 

How To Use Movement in the Fourth Dimension

 

After insight is given into the understanding of how and why a fourth dimension could exist, the question of how one could move through a spatial fourth dimension is frequently raised: and many scientists have sought to give an answer to this question. Imagine a hose that is quite long but thin in width and height; from a far away distance, the hose may seem almost one dimensional, and that is because the other dimensions seem to be almost virtually nothing. When seen at a closer distance, it will actually have visible height and width, which makes it much clearer that it is in the three dimensional space. Making this analogy into a more abstract perspective: these new dimensions could be so small that it is impossible to see and visualize what they may look like, and how they would interact with many objects. This is also strengthened by the knowledge of no current microscopic technology to detect or make another dimension visible. No proof is available from these observations, which can make it seem like the whole idea of another dimension is tomfoolery and not to be dealt with at all. But: by taking the concept of moving through this dimension into another manner - using part of the flatland example - it can be thoroughly thought through. Connect two toruses (also called doughnuts and rings) together and make them highly interlocked in a fashion that deforming the material is impossible, this is an impossible situation, but it is reasonable. Now, the question is: how could you separate them? Using the fourth dimension makes this situation possible, and to start it requires an understanding of what this would look like through the second dimension. A pair of interlocking figures in the second dimension are provided as a model, and it is impossible to separate them just using the second dimension, and will instead require a movement out of the dimensional plane and back into after movement. Drive this conclusion to the rings, and one can have a positive direction moved in the w axis, be moved over in one of the other axes for human space, and be moved right back down in a negative amount with the same absolute value as the previous movement. Extending this to previous statements, it will be evident that the ring will look like it is increasing and decreasing in size accordingly to previous statements. How to visualize how it actually will move is a little harder, and will require multiple images to explain, and to do this each image needs to have a new origin for the w axis to be zero for each new image. Parts of this visualization have a new colour for each new axis and image, and an analysis could be provided to give an understanding to this system of making the movement provided work together with one’s brain. These movements each describe a different time when the rings move through the space which makes a whole visualization of how it may look possible, and understanding this can also aid with understanding what tesseracts or hyper-objects may appear to look like. Like how a hypercube looks when it is rotating. Generally putting all of the pieces together of the previous discussions can be aided with the idea of what an object moving through the new w axis would be like and look like, which scientists are even trying to figure out today.

 

 Ways of visualizing the interlocked rings puzzle.

 

Reaching Out

 

For this specific section of research, a more knowledgeable person from UoC majoring in astrophysics for a second year - called Sebastien Wagner - has been asked four questions about this specific topic. All responses will be listed out in a question and answer fashion.

 

Question 1: What do you currently understand about a fourth dimension?

 

Answer 1: When considering the 4th dimension, the first thought that comes to mind is the physical appearance of 4th dimensional space. But let's start with 2 axes, x and y. Great! You have 2 dimensional space. Now add depth/ third direction, let's call that the z direction. You now have 3d space and for simplicity sake we can imagine a cube. Now let's add a 4th direction, let's call it w, how does this affect our cube? It has length, width, height, it has volume but what can I add to the cube to turn it into a 4th dimensional object. Let's consider a particle as it moves through 3d space, we know its position (xo,yo,zo). And we can measure its change position as time moves on (xo-x,yo-y,zo-z) . We can trace the path of this particle as it moves through space with respect to time. But this particle cannot reverse in time nor increase the rate at which time is moving relative to its movement.  Since we are in 3d space, time is independent of our movement, however you can imagine that time is in fact the spatial direction in 4 dimensional space. Entities in the 4th dimension move freely through time, it is not linear to them, it is not independent of their movements, I am assuming that these 4 dimensional entities can do what I described our particle could not do. 

 

Question 2: With the current information you have, what is your opinion on the concept of a fourth dimension as time and/or space?

 

Answer 2: The concept of the 4th dimension is certainly abstract. It is constructed from our current understanding of our own physical space and some creativity. Mathematically the 4th dimension is not different then any other dimension as in, calculus, linear algebra essentially all of arithmetic works in any dimension, and the rules that define mathematics/ the discrete math, the proofs are the same.

 

Question 3: Using the concepts of both of these ideas of further dimensions: how would they impact the motion of objects and the mathematics describing them?

 

Answer 3: The motion and physics of such objects might also remain the same but with the addition of a few variables, scalar quantities cannot be affected and vectors like direction and velocity will now have one more direction, however the idea remains the same. 

Geometric objects certainly have changed, there is a whole field in science dedicated to special geometry and are unbiased to the dimension, I believe it's known as topology although those whose study topology understand that a donut and a coffee mug are the same shape by definition. I'm delving into a can of worms. 
 

Using the information from these answers, an analysis provided can give great insight into the mind of someone with greater experience than one may find in an individual in ninth grade. Along with the rest of the information: this section has provided better understanding and thought into the possibilities of the fourth dimension.

 

Data

After conducting research, an answer can be formulated from the various problems and insights gained in the vast topic of the fourth dimension; this question being answered is: “What are the principles of movement in the fourth dimension?” From all of this information it can be said that the fourth dimension might exist, in both ways of time and space. Justifications have strengthened both arguments, and it is most likely in current understanding that both are true in nature, even though string theory probably will not always hold - but the extra spatial parts may - and time as a dimension adds so much true information. Physics does not change as much as initial thought may have speculated in current equations, but new equations that interpret how objects can move in and out of the four-dimensional plane significantly help. Thinking of time in the specific ways provided also ended up in the creation of a new way of thinking about how space operates with time in a spacetime plane, and how everything warps spacetime around itself. Spatial extensions to the known universe also allowed for significant portions of physics to be incorporated into it. Unfortunately, in the prospect of current equations, a portion of them had no changes, while most of the ones relating time lead to the same conclusion and effects due to it. But, in the idea of new applications and interpretations: objects significantly changed within the boundaries of visualization, ideas of geometry, shapes of the universe, and the concept of how other dimensions can exist. How to move in the fourth dimension is solved within how perception of lower dimensions compare with higher dimensions, and these present applications to use movement in the fourth dimension. Applications being more important can also imply that older math will have to change and reform itself to describe a new concept, along with new ways to understand, communicate, and interact with the ideas of moving forward. Going further into this: this is due to the new nature of this next dimension, like how sine and cosine require an angle to determine the amount a vector applies in a certain axis, but if there is no angle visible it is impossible to use the implemented principles. Instead one could try to visualize it by moving the origin each time to match it when doing it arbitrarily, but in real life knowing what certain shapes look like through cross-sectional movements at certain speeds will provide direction and magnitude much better than arbitrary understanding. Using previous dimensions as viewpoints for higher ones also contributes to understanding, which should continue to be used to help describe objects more complex in these higher dimensional areas - and this is proven by using the patterns from the hypercube. Luckily, even though there is no evidence from experiments to prove the theory largely being discussed, much proof can be found within the mathematical equations made from this exploration, and how they work together with three-dimensional viewpoints - and not just within string theory. From the research conducted much can be concluded and argued on how it can properly apply the questions, and interpret how they apply to the current conclusions of how space works.

 

Conclusion

After doing significant and tedious research, the question “What are the principles of movement in the fourth dimension?” can be answered and reflected in comparison to the previous predictions from the hypothesis. Explaining the answer: there are several parts to it, but the most significant part is that it depends on which definition one believes in, whether it is both, none, or just one. In the definition of a time dimension, it interprets that everything can only move with time, and that even though reversing it is known to be impossible: it has enough as a magnitude and direction. Rules of relativity also come into play when considering time as a dimension with the principles of spacetime, time dilation, being relative, travelling in time and space, and many other now important concepts to understand to grasp the nature of the universe itself. When applying these concepts to mathematics however, equations need to be brand new, and the old ones require the simplifications of non-light speeds, and other specifications. The understanding of an additional spatial dimension also makes a list of changes to how perceiving can be done with several methods that extend the sight using comparisons from smaller dimensions. Ludicrously proving the theory and confirming it will also in return prove the aspects of string theory with the concepts that are important to understanding the universe like branes, but also needs to be achieved with understanding the patterns and kinds of hyper-objects that can form from these applications. Movement in these perspectives requires advanced applications of geometry and trigonometry, and understanding of the visuals that are provided from using principles can also be achieved with equations. Stating the answer has provided confirmation of the various research committed to, and how the future can use these specific applications - and now a review of the hypothesis will provide a greater conclusion to what was learned. Using inference from the hypothesis, it is evident that there was only one dimension that was considered, and this was a fourth spatial dimension; and it was thought that mathematics would significantly change. Both of these educated assumptions were wrong, as they both had an oversight, with the former not considering that a spatial and time dimension exist, and with the latter not considering that the math that is used for simpler situations can’t change to fit the new situations of time and space. New equations are required in these situations. Additionally, the statement about the impossibility of visualizing it was false in a way, because it is implied so by the common populus, but it is considered by many physicists to actually be possible through the manipulation of origins, cross-sections, and two-dimensional comparison. Claiming that it was also impossible to visualize movement is a little more correct, but with understanding the complications: understanding the time, change in size, and relativity of these concepts will greatly impact the ending result of understanding. Some correct inferences were made though, these specific three predictions are that there is more than just a coordinate system to a fourth dimension, a significant change will need to be made to perception to make visualizing the fourth dimension possible, and there will have to be new tactics to achieve this. In several instances: there were right and wrong predictions. Overall, understanding the answer to the question provided for the project will help understand the intricacies of such a perplexing concept, and the reflection of previous thought will clarify the various kinds of knowledge gained.

 

Citations

 

 

Acknowledgement

I would like to acknowledge the following individuals with the basis on several ideals and efforts - but the most significant contributions will be listed.

  • Sebastien Wagner for completing questions that I needed an opinion from a person who is more developed in the field, and for helping me with consultation with general project assistance like fact checking

 

  • The Saint Joan of Arc staff who participated in making my arrival to the competition possible and with the uttermost effort. Beneficial opportunities to engage in science clearly where shown in school and outside in the CYSF.

 

  • Lastly, my mother whom has always been trying her hardest to do the best for me and all others around her. Without her necessary assistance throughout my life: I simply could not be here.

There are many others who have shown kindness and benevolence through the making of the project, and I wish to thank them too.