1. Introduction

In a digital world, pen-and-paper writing has become increasingly less popular. However, research indicates that traditional longhand writing offers significant advantages over typing, particularly in memory retention [1]. 

2. Research Question and Hypothesis

How can a pen without external components effectively digitize handwritten notes on paper in real time?  

     It is hypothesized that the synergy of low-cost sensors embedded in a pen along with data processing carried out by open-source and ad hoc algorithms can ensure a seamless digital replica of handwriting on a drafting page without external components.

3. Design and Methodology

3.1 Hardware 

To accurately compute and process the position of the pen’s tip, the pen is equipped with the following instrumentation (Figure 1): camera, digital gyroscope, compass, optical mouse sensor, microcontroller, battery, charging port, and wires.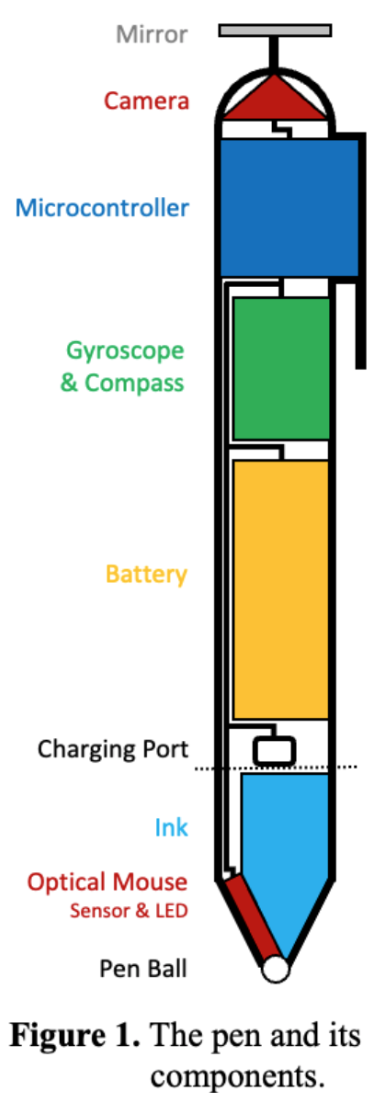

     The camera is mounted at the top end of the pen. The orientation of the camera is parallel to the pen’s axis ensuring that images captured will project the pen’s tip at the central pixel. To facilitate the camera’s power supply without obscuring the scene with wires, the camera will face up and a mirror located at the top of the pen will reproject the drafting page onto the camera. Images will be corrected for distortions introduced by the camera’s lens (tangential and radial) and the mirror [3]. The corresponding distortion coefficients will be derived after processing images of a checkerboard grid during a one-time camera configuration. These coefficients will then be used to autocorrect all future images taken by the camera.

     The digital gyroscope is integrated into the body of the pen to calculate its three-dimensional orientation, specifically measuring the angular deviation of the pen's axis from the normal vector of the drafting page. Gyroscope calibration takes place during the pen's initialization phase, as outlined in Section 3.2.1.

     The compass is integrated into the body of the pen and its role is to calculate the direction of the pen related to the drafting page. The compass undergoes calibration at the initialization phase, as outlined in Section 3.2.1.     

     The optical mouse sensor is mounted at the bottom end of the pen facing the ball. Its role is to accurately trace the movement of the pen’s tip, while in writing mode. 

     Data collected by the above sensors will be transmitted to the microcontroller through a network of wires. The microcontroller is integrated into the body of the pen and its role is to process all input data, calculate the instant locations of the pen’s tip, digitally encode the written scripts, and transmit the digital replicas to an external computer device via Bluetooth communication.     

     The pen’s battery will provide the sensors and microcontroller with power. The battery will be recharged through a designated charging port. The ink cartridge and charging port will be accessible by detaching the bottom end of the pen, along the dotted line in Figure 1. 

3.2 Software 

As shown in Figure 2, a sequence of software modules is carried out in the following order to create the digital replica of the handwriting: initialization of the pen, positioning of the pen’s top (camera’s center point), positioning of the pen’s tip, tracking of the mouse cursor’s movement (while in writing mode), and digitization of written scripts. After the initialization phase, an iterative process alternates between two consecutive states of the pen: down (writing mode starts) and up (writing mode pauses). The following subsections describe the software modules in more detail.  

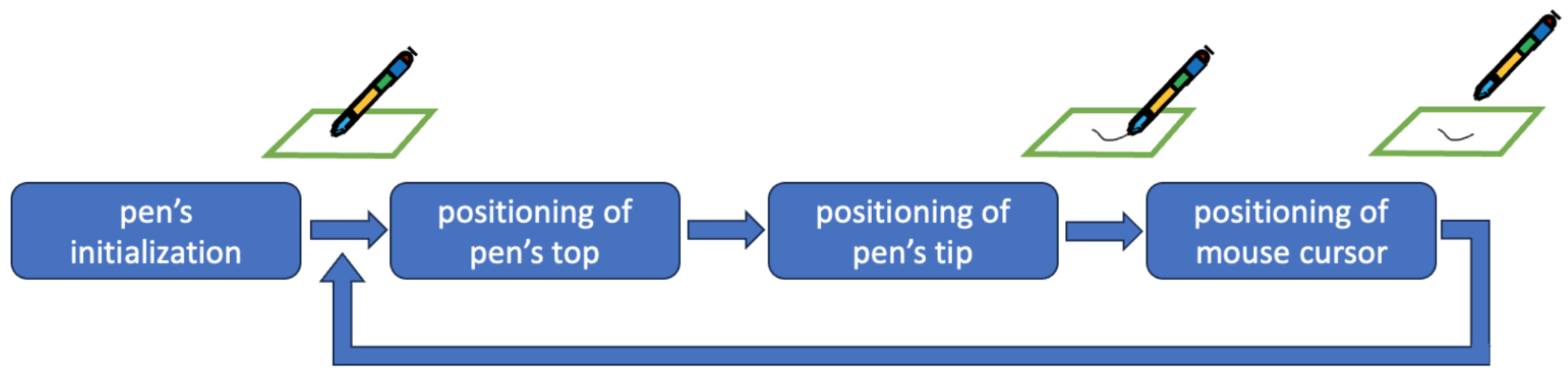
Figure 2. The sequence of modules and the iterative process for pen digitization. 

3.2.1 Initialization of the pen

The initialization phase is carried out in two steps to calibrate the pen’s sensors and capture the drafting page’s properties, respectively.

     The calibration of both the gyroscope and compass is carried out in the first step, as shown in Figure 3a. By aligning the pen with the relative left or right edges on the drafting page, the reference angular origin of the compass and the reference plane for the gyroscope (and the corresponding normal vector of the drafting page) can be calculated. The camera will also collect sample color signatures to identify the color range of the drafting page. This color range will be used as an input parameter to facilitate the image segmentation process, as explained in Section 3.2.2.

     The second step of the initialization phase calculates the dimensions of the drafting page, i.e., the size of the short and long edges. By placing the pen on the page so that the camera has visibility to at least three corner points, as shown in Figure 3b, the page’s dimensions can be calculated. The calculations are described in Section 3.2.2, as they are relevant to those applied for positioning of the pen’s tip.  

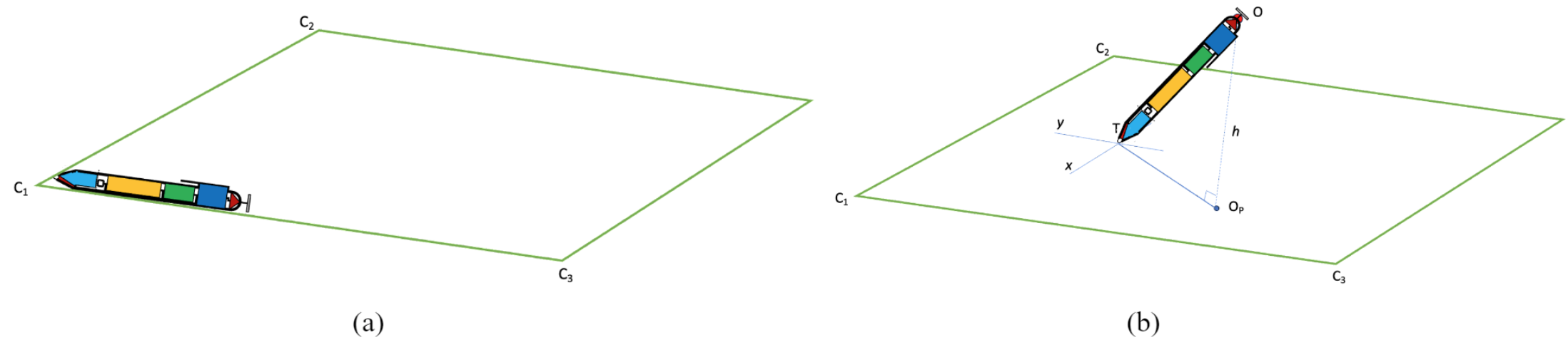
Figure 3. Initialization of the pen: (a) step 1, and (b) step 2.

3.2.2 Positioning of the pen’s top 

The camera will capture wide-angle images, which can be processed to determine the position of the pen’s top (camera’s center point) using the corner points of the drafting page.  

     First, a color segmentation method will be applied to separate the drafting page from the image background. For this task, a well-established algorithm known as Random Walker segmentation [4], available in the OpenCV Python library [5], will be adopted. The color range of the drafting page (captured at the initialization phase; Section 3.2.1) will serve as an input parameter for this algorithm to ensure more accurate segmentation. 

     Next, a conventional corner detection algorithm, known as Harris Corner Detection [6], also available in the OpenCV Python library [5], will be applied. This algorithm will identify the location of the page’s corner points on the image. 

     Given a camera with focal length f positioned at a height h from the drafting page, pointing perpendicular to point O_P, the three corner points C₁, C₂, and C₃ of the page will be projected onto points C^’₁, C^’_2, and C^’₃ in the image, as illustrated in Figure 4a. The formulas in Figure 4b, derived from similar triangles (OO_PC₁ and OO^’C^’₁) and (OO_PC₂ and OO^’C^’₂) associate the page dimensions with the corresponding image projections. By measuring the lengths of these projections in the image, the dimensions of the page can be calculated. 

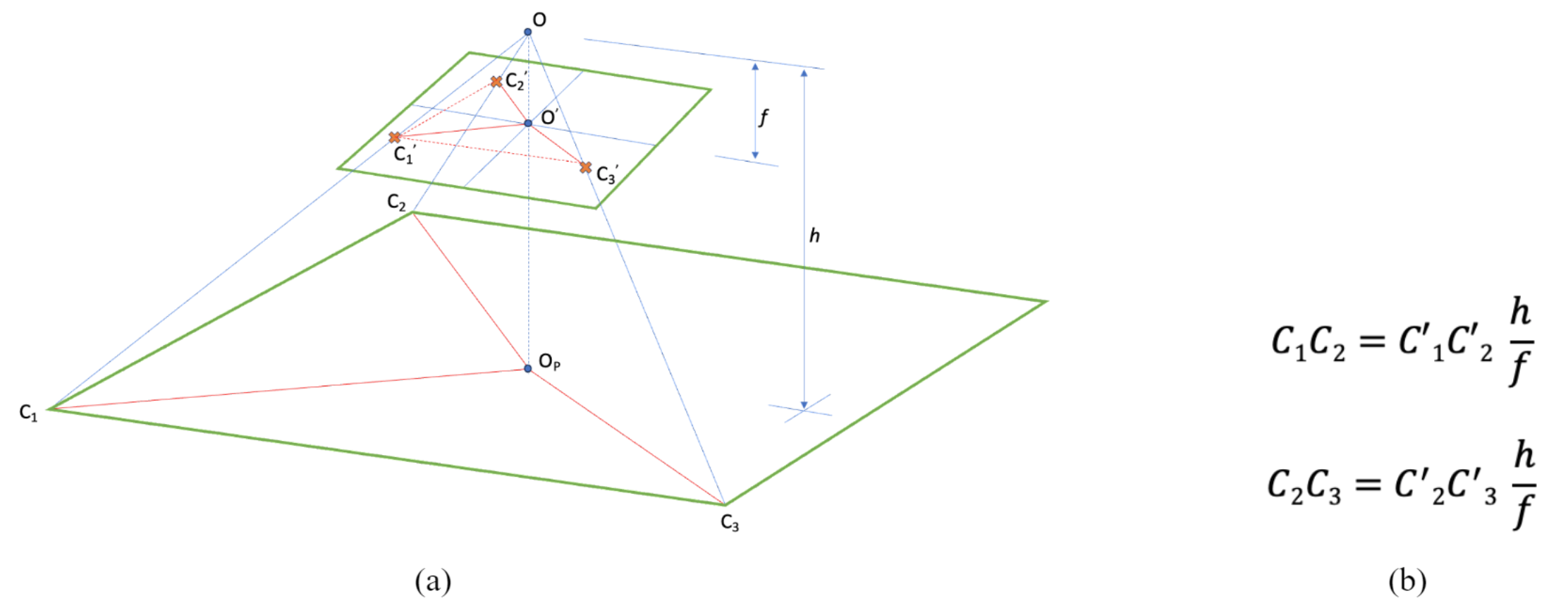
Figure 4. Geometry for a perpendicular pen (h equals the pen’s length). 

     In general, the pen’s axis is not perpendicular to the drafting page [7]. To calculate the position of the pen’s top, the tilted image needs to be rectified so that the formulas in Figure 4b are still valid. The image rectification involves a projective transformation based on the pen’s tilt and rotation angles calculated by the gyroscope and compass. A common image rectification algorithm, known as Warp Perspective Transformation [8], also available in the OpenCV Python library [5], can be applied to rectify the image’s geometry. Figure 5a shows the initial orientation, the direction of the pen, and the image captured by the camera (represented with a small circle and triangle). Figure 5b shows the rectified image as a result of three angular corrections that turn the pen’s axis perpendicular to the drafting page. 

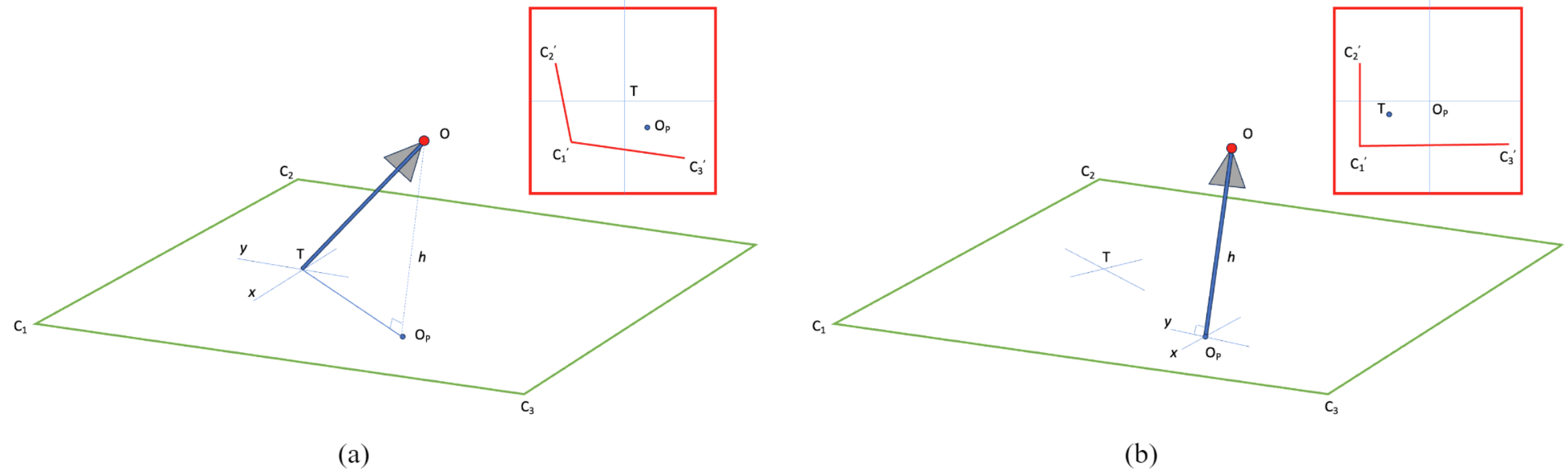
Figure 5. Rectification of the image by turning the pen’s axis perpendicular to the drafting page.     

     Figure 6a shows the geometry of a page with its three corner points  C₁, C₂, and C₃ projected as C’₁, C’₂, and C’₃ onto the rectified image. The formulas in Figure 6b calculate the coordinates of the pen’s top as a function of the short dimension (d) of the drafting page. Notice that these computations require the camera to capture only two corner points of the drafting page. The measurements of the compass can be used to identify which pair of corner points (and corresponding dimension; short or long) are depicted in the image.  

     The calculation of the drafting page dimensions can be carried out at the initialization phase and by applying the same configuration and formulas. From the similar triangles in Figure 4a the short dimension C₁C₂ is given by the formula: C₁C₂ = C^’₁C^’₂ h / f, where h represents the actual offset of the camera from the page and can be extracted by rearranging the formulas in Figure 6. Similarly, the long dimension C₁C₃ can be calculated. To calculate both the short and long dimensions of the drafting page, at least three corner points must be captured from the camera at the initialization phase.    

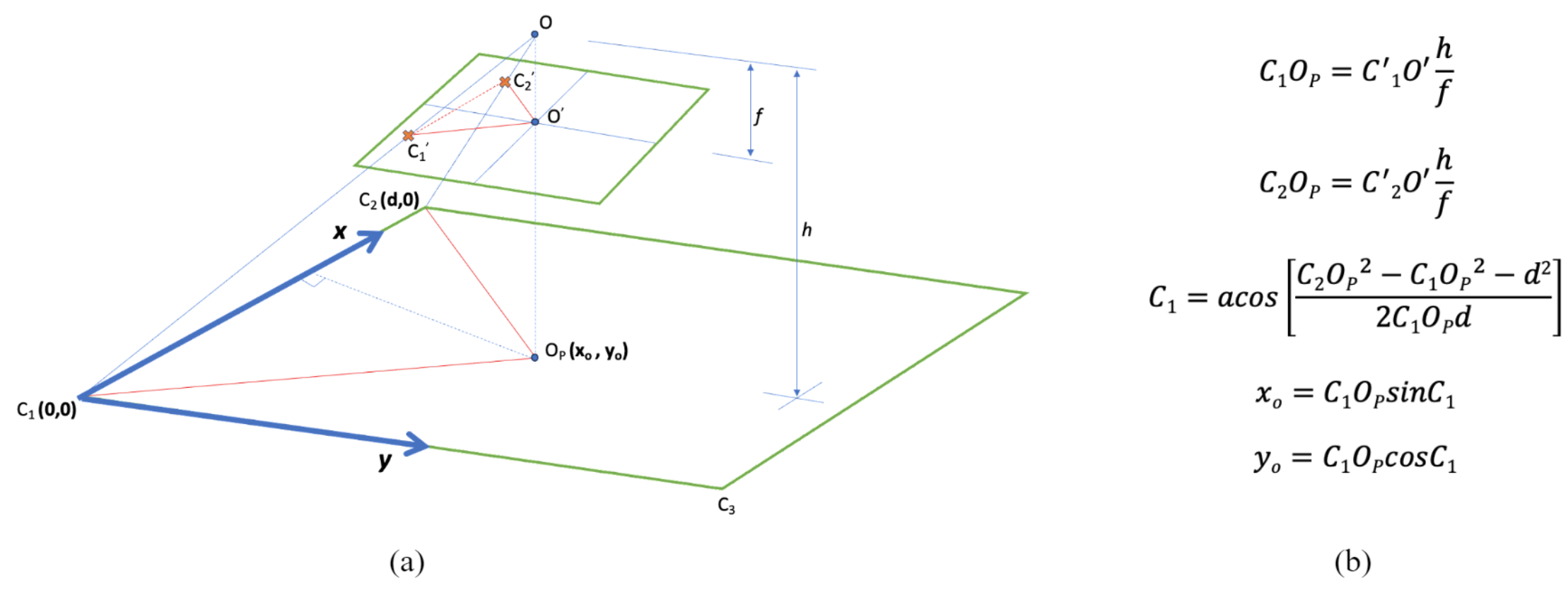
Figure 6. Calculation of the pen’s top coordinates from the rectified image.   

3.2.3 Positioning of the pen’s tip

Given the projection of the camera’s center (pen’s top) on the drafting page O_P(x_o,y_o), the adjusted rotation angle provided by the compass φ_x, and the adjusted tilt angle provided by the gyroscope φ_z as shown in Figure 7a, the coordinates of the pen’s tip T(x_T,y_T) can be calculated using the formulas in Figure 7b.

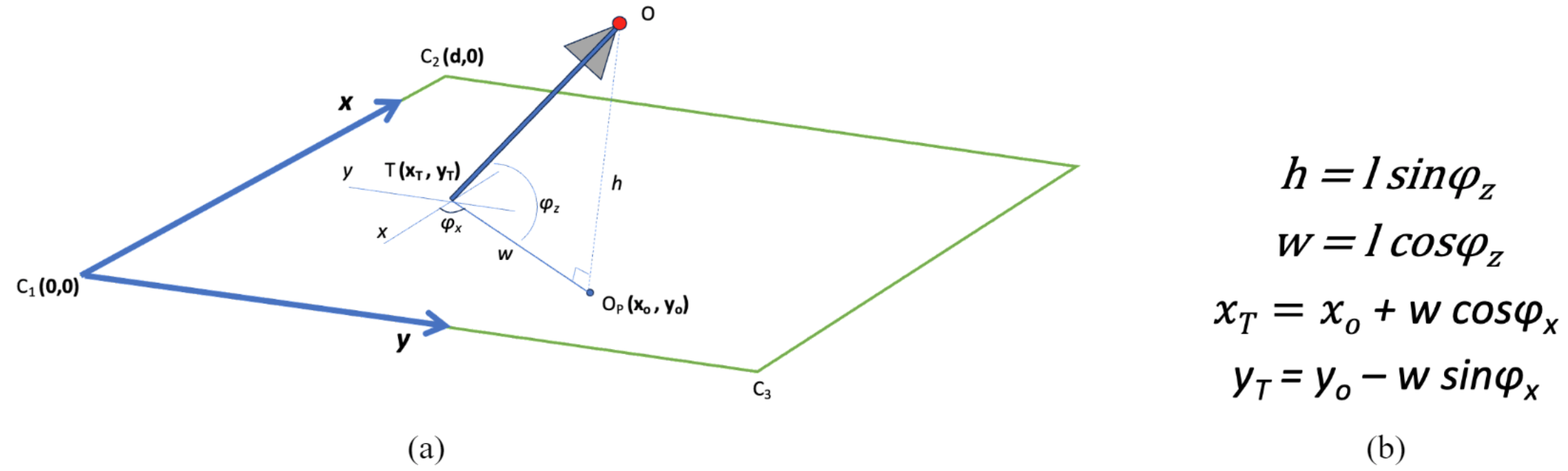
Figure 7. Calculation of the pen’s tip coordinates.

3.2.4 Tracking of the mouse cursor movement and digitization of written scripts

When the pen is in writing mode, the pen's ball rotates through friction, releasing ink from the cartridge. This rotation is detected by the optical mouse sensor which traces the position of the pen’s tip and synchronously transmits this data to the microcontroller for further processing. 

     To translate the mouse cursor to actual distances on the transcription, both the physical size of the drafting page and the mouse sensor’s resolution are required [9]. A designated software program running on the microcontroller will carry out the corresponding calculations. These calculations combined with other sensor data will position written elements onto the exact location in the digital replica of the script.

4. Implementation

Transitioning from theoretical design to practical application is a crucial step toward improved precision and functionality of the device. To facilitate this transition, I acquired the Arduino Nicla Vision ABX00052 [10] (with an embedded camera and 3-axis gyroscope) and the GY-271 HMX5883L Compass Magnetometer [11] (Figure 8). In the subsequent sections, I will present the processes and algorithms developed for the prototype.

Figure 8. The microprocessor (left) and compass (right).

4.1 Image processing 

To accurately detect corners on a drafting page, the image captured by the camera must be processed following the steps presented in Figure 9. The implementation includes a Python notebook (see the attached file) developed in Google Colab that consists of a sequence of modules to carry out these steps as explained in the next sections.

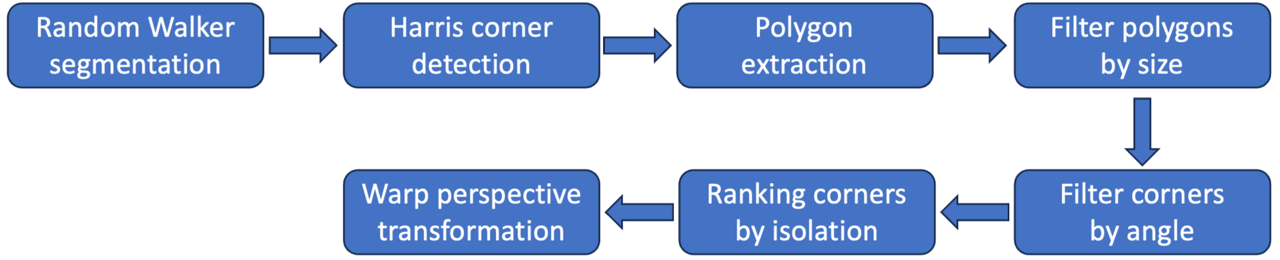
Figure 9. The image processing steps.

4.1.1 Random Walker segmentation

As described in Section 3.2.2 the random walker segmentation algorithm will first be applied to separate the drafting page from the image background or foreground by extracting all areas of the image with a color similar to the drafting page (e.g., white color) as identified in the initialization phase (see Section 3.2.1). Figure 10 presents the result of this step for an example image. 

Figure 10. Example of the image segmentation to extract all areas of the image in the RGB range [220|220|220, 255|255|255]. 

4.1.2 Harris corner detection

This step will identify the location of the page’s corner points for all areas on the image separated in the previous step. This will be accomplished by applying the Harris corner detection algorithm (see Section 3.2.2). Figure 11 presents the outcome of this algorithm for the segmented image in Figure 10. 

Figure 11. An example of the corner detection for the segmented image in Figure 10. All corners have been colored in red dots (number of detected corners: 21,819). 

4.1.3 Polygon extraction 

This step will further process the segmented image to extract contour lines (i.e., segments) that form polygons enclosing the extracted areas (Section 4.1.1). This step will be accomplished using an existing function available in the OpenCV library.  Given the complexity of the geometry, the number of contours will be very high as shown in Figure 12. 

Figure 12. Extraction of polygons from the segmented image in Figure 10. The blue dots show the corner points and the green lines (wherever visible) show the polygon outlines (contours).

4.1.5 Filter corners by polygon size

This step will minimize the noise by filtering the vertices (corners) for all tiny polygons generated in the previous step. This is accomplished by calculating the area of all polygons generated in the previous step and eliminating those polygons (and their corner points) with an area smaller than a threshold area value. Figure 13 shows the result of this step for the polygons in Figure 12.

Figure 13. Filtering the corners for all polygons in Figure 12 with an area smaller than 100 sq pixel size. This results in two polygons delimited by 3 and 4 vertices.  

4.1.5 Filter corners by angle

As the edges are expected to meet at the corner point of the page in a right angle, those corner points of the polygons generated in the previous step with an acute or obtuse angle will be irrelevant and can be eliminated. Figure 14 shows how the corner points in Figure 13 can be filtered by angle. 

Figure 14. The corner points in Figure 13 with an angle outside the range [70-110] degrees have been colored red. 

4.1.6 Ranking corners by isolation

There are corner points that meet the angle condition in the previous step without being located at a page corner. An example is point 1 at the left polygon in Figure 14. To eliminate these points, their vicinity will be tested against the corner points generated by the Harris corner detection (Section 4.1.2). Corners located in non-page corner positions always have more noise (i.e., points generated by the Harris corner detection) in their vicinity, due to the higher complexity of local geometry. Based on this observation, all eligible (blue) corner points as filtered in the previous step, will be ranked in the reverse order based on their local level of noise. The level of noise corresponds to the total number of the points detected by the Harris algorithm (shown in Figure 11) falling within a range of 5 pixels along x and y axis around each eligible (blue) point. The top two corner points, i.e., those with the least noise in their vicinity will represent the page corners. Figure 15 shows the two most isolated corners for those (blue) corners generated in Figure 14. These corners will be used as a reference to compute the location of the pen’s tip (see Section 3.2.3).   

Figure 15. The two page corners as identified by ranking the blue points in Figure 14 (colored as green dots). 

4.1.7 Warp perspective transformation

The last step of the image processing involves the geometric rectification of the tilted image to the vertical. For this step, a Warp perspective transformation will be applied (see Section 3.2.2). Given the three-dimensional rotation parameters of the camera as calculated by the embedded gyroscope, an algorithm from the OpenCV library will be used to implement the rectification (Figure 16).

Figure 16. The result of the Warp perspective transformation of the image in Figure 15. The 3D rotation parameters around the axes x, y, and z were reported by the gyroscope as: (25, 3, -31) (in degrees).

4.2 Testing gyroscope accuracy and drift

A gyroscope measures angular velocity rather than directly measuring angles. By integrating angular velocity data over time, one can determine the angular displacement. Accurately measuring the gyroscope's precision using manual methods, such as a protractor, introduces a significant margin of error. Therefore, this experiment will not focus on the immediate accuracy of angular displacement measurements but will instead assess the long-term drift of the Arduino Nicla Vision’s 3-axis gyroscope (specifically, the LSM6DSOXTR model from STMicroelectronics). This will provide insight into the gyroscope's stability and reliability to ensure that the gyroscope's readings accurately depict the pen's orientation throughout its operation.

Materials:

- Arduino Nicla Vision with the LSM6DSOXTR 3-axis gyroscope

- Computer with OpenMV [12] installed (where I will collect and record data from the Arduino)

- Thermometer (to ensure a consistent temperature testing environment)

 

 

Figure 17. The materials used in the experiment.

Variables:

- Independent: Time

- Dependent: Angular drift readings from the gyroscope in 3 dimensions

- Controlled: Environmental temperature, device placement stability

Setup:

I secured the Nicla Vision on a stable, non-moving surface to eliminate any external influences on its orientation. I monitored and recorded the ambient temperature throughout the experiment to ensure it remained constant, recognizing that temperature variations could impact the sensor's performance. The device was undisturbed during the data collection period to avoid any artificial introduction of angular displacement.

Data collection:

I performed a series of experiments to collect angular measurements for temporal intervals of 10 minutes with a frequency of 10 readings per second to a total of 6,000 rotation values for each of the three dimensions (X-angle, Y-angle, Z-angle). The long interval and high frequency were chosen to capture the writing period on a single page and the movement of the writer’s hand, respectively. 

For the gyroscope to provide precise angular measurements, calibration is required. In the following two Sections, I describe the data collected from the gyroscope in two experiments. The first experiment collects data from a non-calibrated gyroscope with significant drift errors in all three dimensions. This data was analyzed to calibrate the gyroscope for the second experiment, where high-precision measurements were achieved.      

 

Figure 18. Gyroscope calibration and excerpt of the OpenMV code. 

Before calibration:

As anticipated the first experiment reported inaccurate angular measurements given the presence of systematic errors in the non-calibrated gyroscope. As shown in the graph in Figure 19, angular drift will exceed 10 degrees within the first few seconds. The table in Figure 19 reports the average, (signed) maximum, and (signed) minimum differences (dX, dY, dZ) between temporal successive pairs of angular measurements in three dimensions (X-angle, Y-angle, Z-angle). The differences are very similar for each dimension along the 10 minutes and correspond to systematic errors of the gyroscope. The average values listed at the top of the table were used to calibrate (i.e., correct) each measurement in the second experiment (see the code in Figure 18).

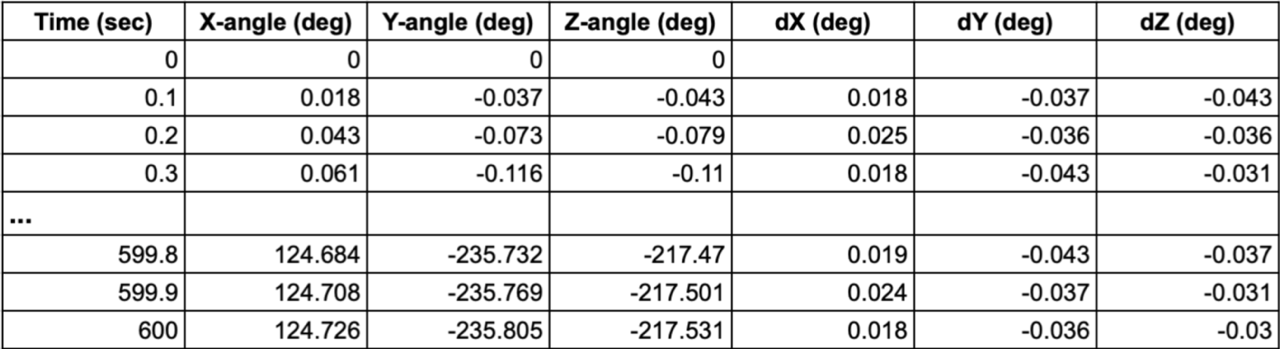
Figure 19. Non-calibrated gyroscope measurements for a period of ten minutes.

After calibration:

In the second experiment, each gyroscope measurement was calibrated using the following formulas (Figure 18):

  calibrated_X-angle = measured_X-angle + dX-AVG,   where dX-AVG = -0.021

  calibrated_Y-angle = measured_Y-angle + dX-AVG,   where dY-AVG = 0.039

  calibrated_Z-angle = measured_Z-angle + dX-AVG,   where dZ-AVG = 0.036

As shown in Figure 20, the angular drift remains very low in all three dimensions and did not exceed 1 degree or 5 degrees after 2 or 5 minutes, respectively. This experiment was repeated multiple times with equivalent angular errors. 

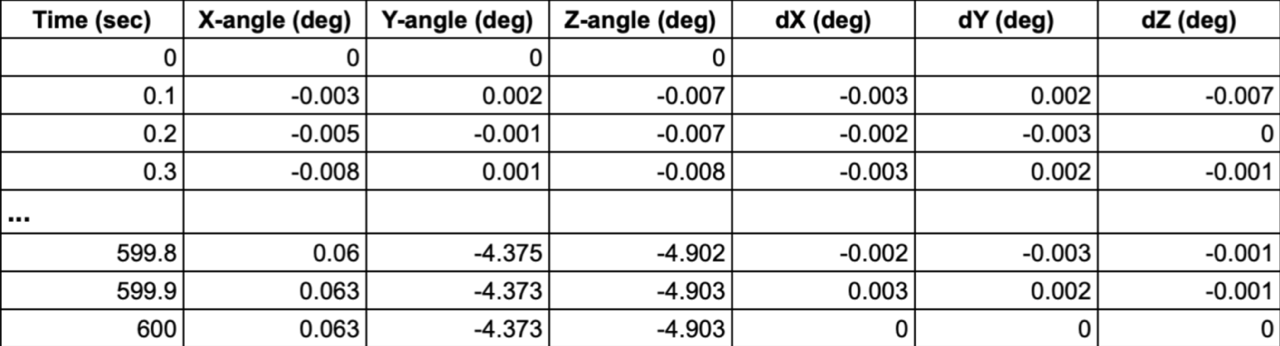
Figure 20. Calibrated gyroscope measurements for a period of ten minutes.

Data Analysis:

The outcomes of the above experiments demonstrate that a gyroscope can effectively be used to compute the pen’s orientation, which is required for the positioning of the pen’s tip. However, the gyroscope needs to be calibrated at the initialization phase to keep the angular errors low. The following Section discusses the impact of angular errors in the positioning of the pen;’s tip.   

4.3 Estimated accuracy

The accuracy of the pen's tilt measurement, determined by the gyroscope, is prone to angular errors. An estimate of the displacement d of the pen's tip caused by an angular error θ of the gyroscope can be derived by the formula d = l sin θ, where l represents the distance from the camera to the pen’s tip. As shown in Figure 21, the displacement can be in any direction. For l = 13 cm, the measure of the displacement ranges from 2 to 11 mm for an angular error θ equal to 1 to 5 deg. respectively.

​​​

Figure 21. Displacement caused by an angular error θ of the pen’s tilt determined by the gyroscope.

5. Risk and safety

Safety will be taken with utmost consideration during the manufacturing and disposal of the pen and its materials. To ensure a safe work environment, proper use and handling of equipment such as box cutters and soldering irons will strictly adhere to safety guidelines regarding precautions, personal protective equipment, and first aid measures [13][14]. Furthermore, all activities will be conducted in a closed environment, as such, proper ventilation will be a top priority, especially during soldering activities. Finally, materials requiring special disposal, such as batteries, wires, and plastics, will be recycled at local drop-off and recycling centers. Any remaining components that do not pose a risk will be disposed of in compliance with environmental standards and regulations [15].

6. Implications

This project seeks to merge the benefits of digital technology and traditional handwriting, thereby fostering cognitive development and educational engagement. Furthermore, the pen facilitates online learning, particularly for students in remote communities, enabling instantaneous sharing and collaboration between peers and teachers [16].

     The significance of this project extends beyond academic domains, including healthcare. The embedded gyroscope could efficiently detect movement abnormalities in the handwriting process and help early diagnosis or monitoring of patients with Parkinson’s disease or those recovering from severe head injury or a stroke [17][18][19]. 

7. Limitations

7.1 Positioning error 

Though sensors embedded in the pen can provide accurate measurements, they have some limitations that can lead to random or systematic errors. The digital gyroscope requires a sporadic initialization as bias instability or noise could cause a significant angular drift [20][21]. In addition, image processing algorithms may become unreliable when light conditions deviate from those present at the initialization phase or when there is low contrast between the drafting page and other adjacent items. 

7.2 Moving the drafting page 

The initialization of the gyroscope and compass sets the angular origin parallel to the direction of the relative left or right edges of the drafting page (Figure 3a). It is assumed that the drafting page will remain stationary during handwriting. Should the page move, the pen must be re-initialized. An external sensor connected to the page could prevent this re-initialization; however, integrating such a sensor goes beyond the scope of this proposal. 

7.3 Computational power

As the computational power of the microcontroller (Figure 1) is limited, some of the processing tasks might need to be migrated to an external device. Data collected from the pen’s sensors as well as processed information will be transmitted to the external device via Bluetooth communication. If the pen’s Bluetooth is off or the external device is temporarily unavailable, all sensor data requiring further processing and/or the processed digital replicas can be saved in the microcontroller’s storage unit and transmitted to the external device when the connection becomes available.

7.4 Battery’s capacity

The pen incorporates multiple high-refresh-rate sensors and a microcontroller for data processing and wireless communication, leading to substantial battery depletion. A high-capacity battery could mitigate the need for frequent recharging. However, this may result in increased size and weight of the pen, compromising ergonomics. An effective alternative is to introduce an automatic power saver when the pen is idle, increasing the battery’s overall lifespan.

8. Conclusion

In conclusion, this project successfully addresses the research question by demonstrating the feasibility of a pen that digitizes handwritten notes in real time without external components. The design integrates low-cost sensors and efficient algorithms to digitize handwriting accurately, thereby combining the cognitive benefits of traditional writing with digital convenience. It is worth noting that this project is currently under active development, with the primary emphasis on executing tasks to establish a proof of concept.

Future developments in implementing my concepts can be classified into short and long-term tasks. 

Short-term tasks include:

- The migration of the image processing modules (currently available in the OpenCV platform; see Section 4.1) to the OpenMV IDE so that the image processing can be carried out on real-time video through the microcontroller's camera.  

- Development of the mouse and compass sensors, and investigation of positioning accuracies and potential limitations. 

- Experimental work on positioning the pen’s tip based on the synergy of the sensors: camera, gyroscope, mouse, and compass.

Long-term tasks include:

- Design and 3D print the pen, incorporate custom hardware components (see Section 3.1), and establish a flawless execution of the positioning.

- Testing, validation, and commercialization of the final product.

References 

[1] Mueller, P.A., Oppenheimer, D.M. (2014) The Pen Is Mightier Than the Keyboard: Advantages of Longhand Over Laptop Note Taking. Psychological Science Online. SAGE. https://doi.org/10.1177/0956797614524581 [Visited on 14 June 2023]

[2] Luckhurst, S. (2018) Livescribe Smartpen: The pen will always be mightier than the keyboard. Arts Computing Office Newsletter. University of Waterloo. https://uwaterloo.ca/arts-computing-newsletter/spring-2018/spring-2018/livescribe-smartpen [Visited on 7 June 2023]

[3] Sadekar, K. (2023) Camera Calibration: Understanding Lens Distortion. OpenCV. https://learnopencv.com/understanding-lens-distortion/ [Visited on 7 June 2023]

[4] random_walker() https://scikit-image.org/docs/stable/auto_examples/segmentation/plot_ random_walker_segmentation.html#random-walker-segmentation [Visited on 23 July 2023]

[5] OpenCV Library https://pypi.org/project/opencv-python/ [Visited on 23 July 2023]

[6] CornerHarris()  https://docs.opencv.org/4.x/dc/d0d/tutorial_py_features_harris.html [Visited on 23 July 2023]

[7] Slama, C.C., Theurer, C., and Hendrikson, S.W. (Eds) (1980) Manual of Photogrammetry. 4th Edition, American Society of Photogrammetry, Falls Church, Va.

[8] ​​WarpPerspective() https://docs.opencv.org/4.x/da/d54/group__imgproc__transform.html [Visited on 24 July 2023]

[9] Ng, T.W. (2003) The optical mouse as a two-dimensional displacement sensor. Sensors and Actuators A: Physical, 107(1) , pp. 21-25. Elsevier. http://doi.org/10.1016/S0924-4247(03)00256-5  [Visited on 3 October 2023]

[10] Arduino Nicla Vision ABX00052 https://docs.arduino.cc/tutorials/nicla-vision/user-manual/ [Visited on 4 October 2023]

[11] GY-271 HMX5883L Compass Magnetometer https://handsontec.com/dataspecs/sensor/GY-271%20HMC5883L.pdf [Visited on 8 December 2023]

[12] OpenMV IDE https://openmv.io/ [Visited on 9 December 2023]

[13] Box Cutter Safety, Environmental Health and Safety, University of Washington.  https://www.ehs.washington.edu/system/files/resources/Box-cutter-safety.pdf [Visited on: Visited on 8 December 2023]

[14] Soldering Safety, Department of Engineering Health and Safety, University of Cambridge https://safety.eng.cam.ac.uk/safe-working/copy_of_soldering-safety [Visited on 8 December 2023]

[15] Inspiring a future without waste. Alberta Recycling Management Authority. https://www.albertarecycling.ca [Visited on 8 December 2023]

[16] Layton, J. (2023) Distance as a Factor for First Nations, Métis, and Inuit High School Completion. Education, learning, and training: Research Paper Series, Statistics Canada. https://www150.statcan.gc.ca/n1/pub/81-595-m/81-595-m2023002-eng.htm [Visited on 9 December 2023]

[17] Lees, A.J., (2022) How Handwriting Analysis Helps Diagnose Parkinson's Disease.The value of a pen and pencil in neurology. Psychology Today. 21 Jan 2022. https://www.psychologytoday.com/ca/blog/brainspotting/202201/how-handwriting-analysis-helps-diagnose-parkinsons-disease [Visited on 9 December 2023]

[18] Adhavi Shri, A.S., Praveen Kumar, S.,  and Aravind, T. (2013) Design of Mems Gyroscope to detect and monitor Parkinson's disease - A study. International Conference on Smart Structures and Systems (ICSSS'13), IEEE Explore, pp. 77-81, doi: 10.1109/ICSSS.2013.6623005

[19] San-Segundo, R., Zhang, A., Cebulla, A., Panev, S., Tabor, G., Stebbins, K., Massa, R.E., Whitford, A., de la Torre, F., Hodgins, J.(2020)  Parkinson’s Disease Tremor Detection in the Wild Using Wearable Accelerometers. Sensors 20, 5817. https://doi.org/10.3390/s20205817

[20] Fraden, J. (2015) Handbook of Modern Sensors: Physics, Designs, and Applications. 5th edition. Springer. 

[21] Encyclopaedia Britannica (Eds) (2023) Gyroscope, Britannica https://www.britannica.com/technology/gyroscope [Visited on 7 June 2023]

I would like to acknowledge Pantelis Stefanakis, Electrical and Computer Engineer for his advice and support throughout my project. His support included helping me validate my research and find effective experimental methods to test the prototype. Thank you to Spiros Ratsiatos, Computer Scientist for walking me through the programming tools used in this project and the debugging of my programming scripts. Finally, I would like to thank George Tritakis, Medical Doctor for his insights on the potential implications of my project in healthcare and safety practices.