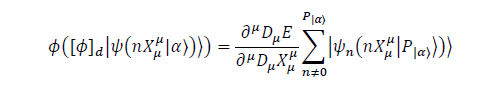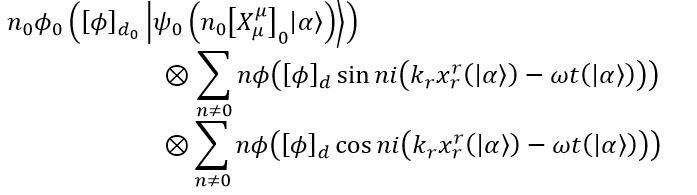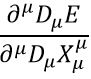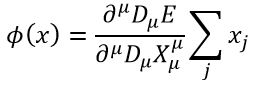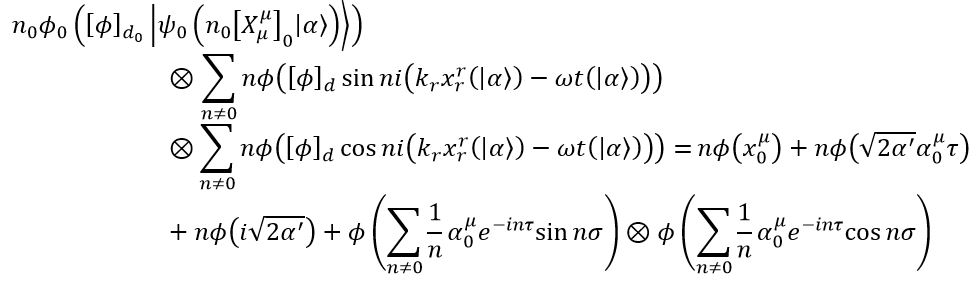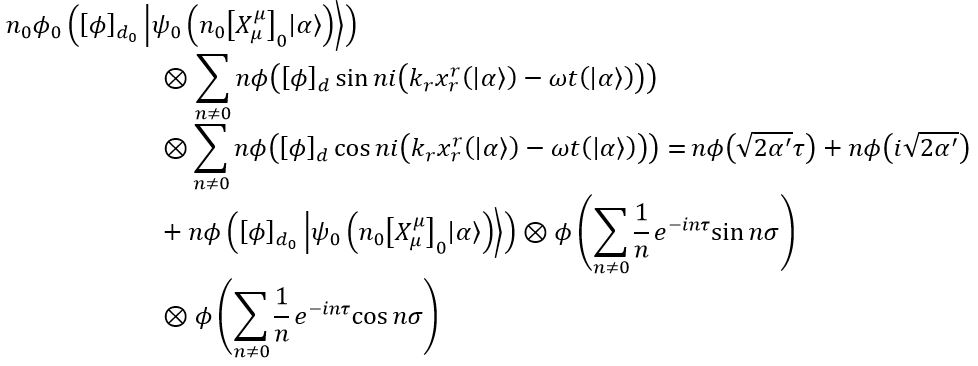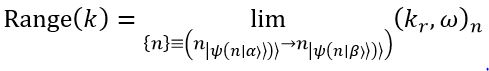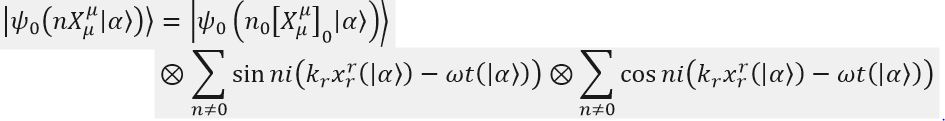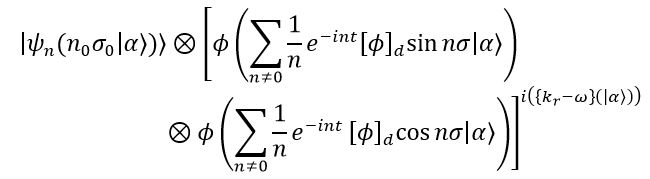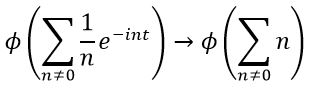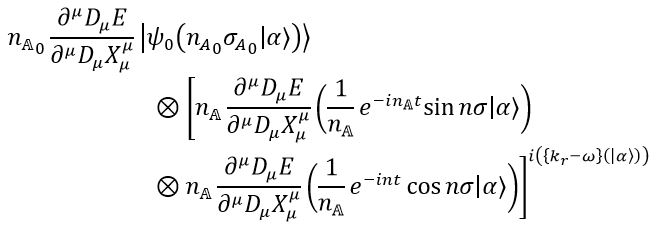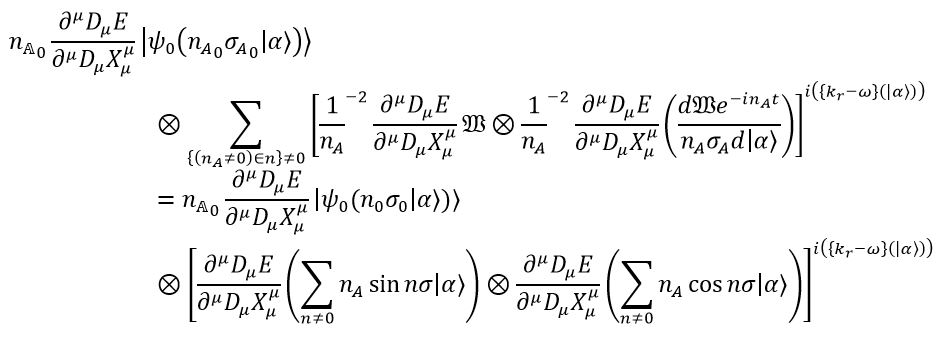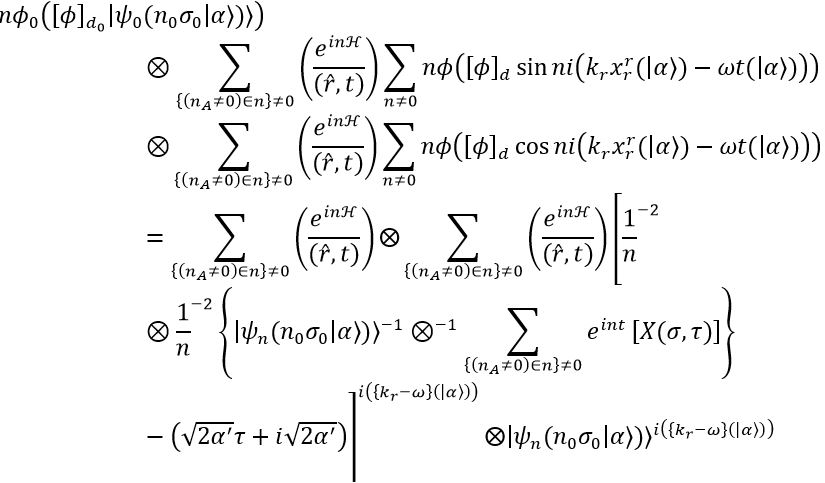1. Abstract.

 

    In December, I wrote many a paper on energy requirements for a proof of string theory and also string theoretic gravitation. As a continuation of those papers, I am writing a paper on a formal proof of string theory. A formal string theory has not been found for many decades. Hence, in this paper I examine a model of string theory where the Fourier series of an arbitrary energy field is equivalent to a relational equation including a string manifold. This leads to new versions of applying Kaluza Klein Theory.

2. Introduction.

 

    Let there be some Energy Field ϕ such that

Where  is the state space for all solutions  that satisfy the "energetic" wave function. Taking the fourier series of the field, and we obtain,

The equality we must create, must therefore be between the above Fourier series of a field and the string theory expansion, operated by 

Which is ϕ such that you can operate it on any x such that

We will have must have that we must find a relational equation, that looks something like (with more operations applied on it)

This is not correct. But we will prove that there exists an equation relating the Fourier series of the field and the field operated the open string expansion, . We prove this by some Wave functional Manipulations, and a proof for the Kazula-Klein theory excluding the Hierarchy Problem in the next part. Our first requirement is to remove the momentum terms due to the fact that our equations must be massless for now. And so,

We are going to modify these equations to find a general equation relating The Fourier series of the FIeld and the Open String Expansion in the reasearch section of this document.

3. General manipulation and a equation for initial terms in the equation         

    Our goal now is to create a wave function from what we have. The first step is a wave number that is energy bounded.

 

Lemma 3.1

    First let us assume that

Now k is bounded by energy levels. Therefore,

Where  is the ground state and  is the maximum energy state. And we will define now that,

END OF LEMMA.

Lemma 3.2

From Lemma 3.1, we can determine that any ψ  must have . Some plugging in will therefore yield us

Knowing this, we have rules for k such that it does not grow to such extreme levels in the equality we want to present.

END OF LEMMA.

Now we shall focus on a conversion of  in the open string theoretic expansion to  in the fourier series of the field.

Lemma 3.3

To accomplish our objective, we must first understand that

And then we derive from the basic definition of the wave function,

We must find an equation that encapsulates the idea that there exists a relation

From the definition of the wave function presented in the second equation in this lemma, some arithmetic gives us

Where we let ,  and  such that

Now, we just put back the  terms and we get

END OF LEMMA.

Lemma 3.4

I will develop a final, smaller lemma to get an equality between the wave function and the terms 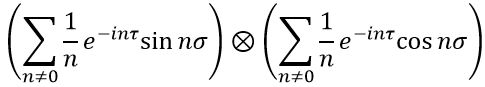 from the open string expansion. From the definition of the open string, we encounter the  terms. Let us now ignore terms like  and consider

Our objective is to find a relation justifying  such that

Realizing that 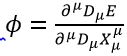, the modified string expansion is therefore,

Realizing that this is just an algebraic operation, to get the required relation, we shall obtain

Where we have an arbitrary n, say,  and an arbitrary σ, say , and . The operations made to get this equation are in the Log-book. Otherwise, these equations imply a relation

This is the relation between the Fourier series and the string expansion.

END OF LEMMA

Therefore, after proving Kaluza Klein theory, T-duality, and certain symmetric theorems in the Standard Model, General Relativity, and Quantum mechanics, we can present a variation on supersymmetric string theories where there exists a Field-Expansion duality (F-E duality).

I have therefore defined a duality between M-theory and Relativistic Quantum Field theory. This implies a field theory of M-theory which can define physical objects. All stemming from relational equations defined in Lemma 3.4. Supersymmetric (and Pertubative) String Theories still require proof for the T-duality found in its framework, proof for Kaluza-Klein compactifications, proofs with large extra dimensions postulated in recent years. I shall continue my researching and provide such proofs in the second part, which will come out at a later time.

I would like to give thanks to my Homeroom teacher (Ms McNutt) for editing and pointing out typos, as well as the joyful, enthusiastic intrest brought to me by my class and friends; also the Science club teachers and Ms. Lai & judges at my school for giving advice on my project. And finally, my mom has been helping and organizing my schedules. I thank you all.